Around King Arthur's Table
King Arthur used to play a game in which a certain number of his knights would sit around a table and King Arthur would start with the knight that was sitting on chair one and say "You're in" and move to chair two and say "You're out". The knights that were "In" would remain sitting, the knights that were "Out" left the table. He continued around the table using this pattern. When he came back around to the knight in chair one he either said "You're in" or "You're out", depending on what he had said to the previous knight. The game would end when there was one knight left and that knight was the winner.
The question we were posed with was if we knew how many knights were going to be at the table, how could we quickly determine which chair to sit in so that we could win?
The question we were posed with was if we knew how many knights were going to be at the table, how could we quickly determine which chair to sit in so that we could win?
The Process
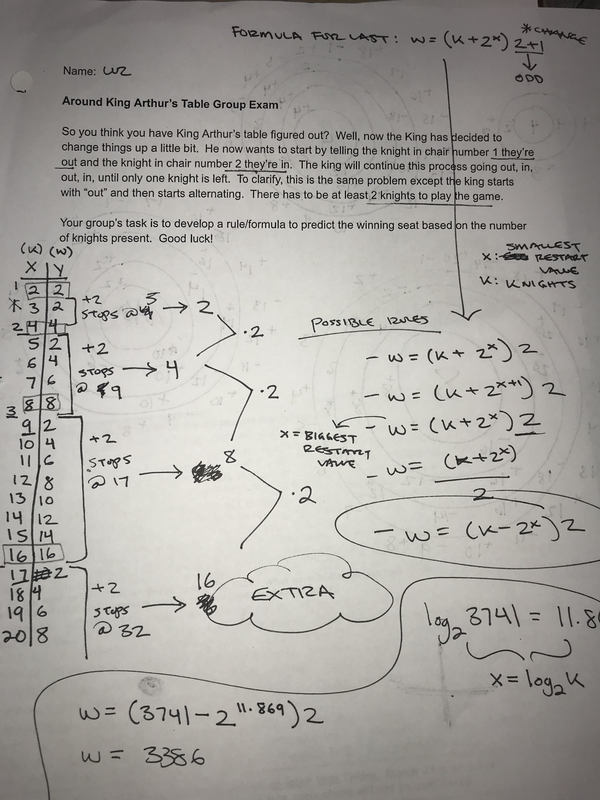
When we were first presented with this problem we spent five minutes alone finding a way that made sense to approach the problem with the ultimate goal of presenting our findings to the group to later develop a rule. I immediately thought of creating a X,Y table in which "X" would represent the total number of knights participating in the game and "Y" would represent the winner of the game.
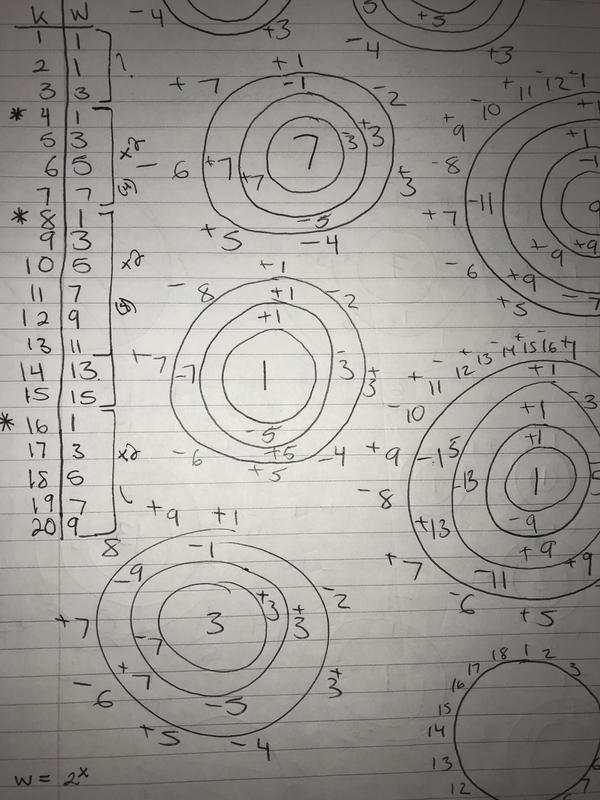
Once my group began to share out our ideas we decided to expand the X,Y table. In order to find the winning knight I drew a circle with the total number of knights on the outside of the circle and the winning knight number in the center of the circle.
We decided to stop filling out the table once we began to notice a pattern in the outcomes of the games. We noticed two major things that would later help us create our formula:
1. Every winner was sitting in a chair with an odd number
2. The pattern under Y increased by 2 and then would "reset" and start back at 1 (Ex; 1,3,5,7,1,3,5,7,9,11,1...)
At the end of the work time the group found that the solution to this problem was W=(K+2^x)2+1
W being the winner of the certain amount of knights playing the game
K being the total amount of knights
X being the smallest restart value
2+1 would ensure that the end value would be a odd number
Once my group began to share out our ideas we decided to expand the X,Y table. In order to find the winning knight I drew a circle with the total number of knights on the outside of the circle and the winning knight number in the center of the circle.
We decided to stop filling out the table once we began to notice a pattern in the outcomes of the games. We noticed two major things that would later help us create our formula:
1. Every winner was sitting in a chair with an odd number
2. The pattern under Y increased by 2 and then would "reset" and start back at 1 (Ex; 1,3,5,7,1,3,5,7,9,11,1...)
At the end of the work time the group found that the solution to this problem was W=(K+2^x)2+1
W being the winner of the certain amount of knights playing the game
K being the total amount of knights
X being the smallest restart value
2+1 would ensure that the end value would be a odd number
Reflection
|
nThroughout the process of trying to find a solution and formula to this problem I struggled most with my ability to notice patterns that I had never seen before. It was obvious that there was "something going on" in the table but because I was not comfortable with this particular pattern I became frustrated and felt like I was unable to solve and understand the problem. I am someone who is very comfortable with asking clarifying questions to my group mates or my teachers, so I began by asking the people around me for support. Through conversation, plenty of examples, and doing work on the board to show our thinking process to each other I began to understand what the patterns meant. Additionally, I was able to help my peers understand concepts that I was comfortable with through these group interactions.
Since the initial stages in solving this problem to our work together on the group quiz, my table has always been able to work efficiently. We were able to express our ideas with each other, made sure that everyone was listened to and understood the material, and was comfortable enough to ask questions throughout the entire process. One can see our group's successes by looking at our latest group quiz. We received full credit because we were on task and came to a solution that we all understood. The group quiz was incredibly helpful to me. I was able to understand concepts that I couldn't grasp in the original problem and even explored old concepts like using "log". If I were to grade myself on my work during this week I would give myself an A. This is because I stayed on task throughout the majority of the work time, I played a key role in helping my groups understanding of the problem, and was always engaging with the material and the people around me by asking questions and making suggestions. |