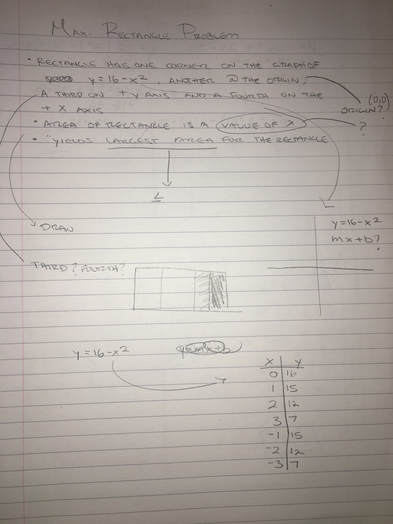
Maximum Rectangle
A rectangle has one corner on the graph of y = 16 - x^2 , another at the origin, a third on the positive y-axis, and the fourth on the positive
x-axis. If the area of the rectangle is a function of x, what value of x yields the largest area for the triangle.
x-axis. If the area of the rectangle is a function of x, what value of x yields the largest area for the triangle.
The Process
When I was first introduced to this problem I was told to take a few minutes after reading the statement to understand the problem and make attempts to solve it. I had no clue as to how to approach it and began to write down questions about words and phrases.
After a few minutes we shared our ideas and questions with the people around us. From the conversation we had as a group we created an X, Y table based on the equation we were initially given. Doing this was our group’s first step toward solving the problem.
After a few minutes we shared our ideas and questions with the people around us. From the conversation we had as a group we created an X, Y table based on the equation we were initially given. Doing this was our group’s first step toward solving the problem.
|
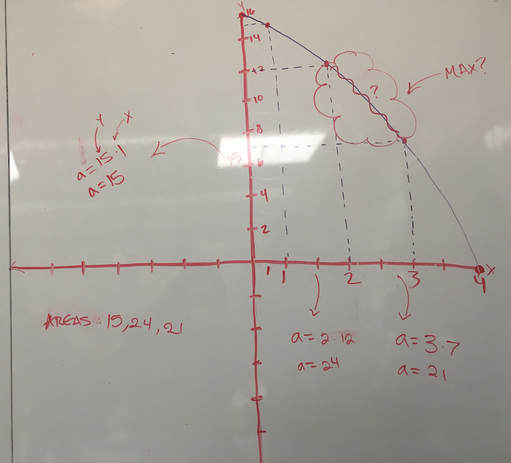
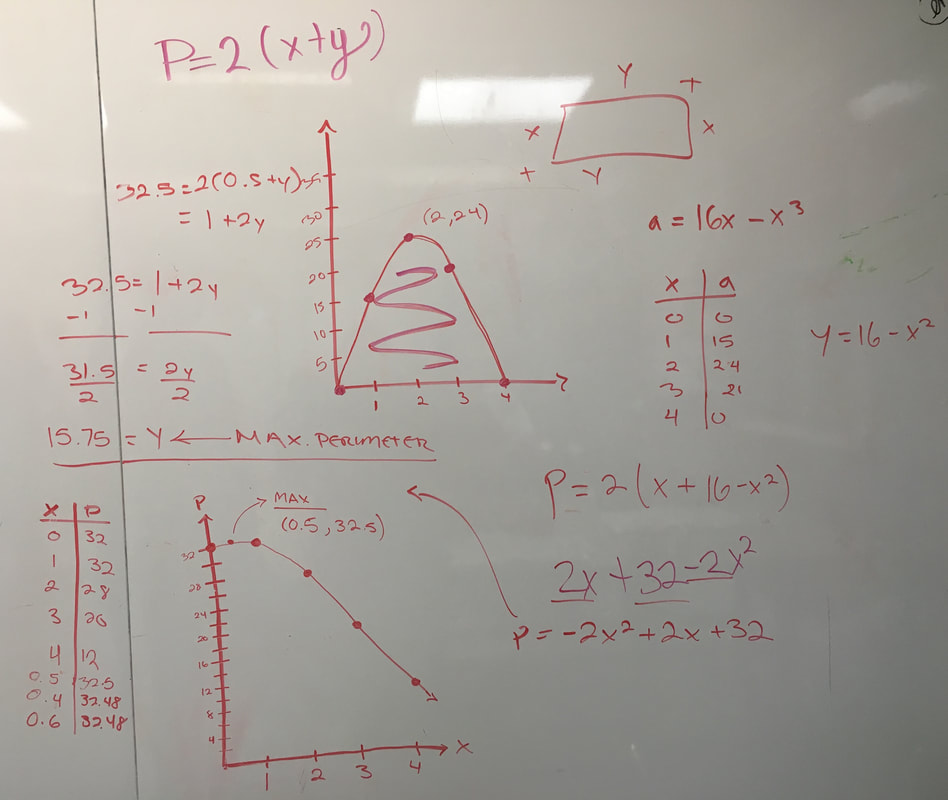
In order to confirm our findings we created equations that made sure our solutions to find the perimeter and area are true. The first equation was A = 16x - x^3. How we found this was by plugging in y = 16 - x^2 to A = X * L, which looks like
A = X ( 16 - x^2 ), and distribute. By doing this and plugging in the side length of the rectangle to the equation, my group believes that the maximum area to our rectangle is 24.6. In order to find the value of the maximum perimeter of the rectangle my group applied a similar strategy to how we found the maximum area. We started with understanding how to find the perimeter of a rectangle, which is P = 2 ( X + Y). With this we plugged in our original value of Y and ended up with P = -2X^2 + 2X + 32. After graphing this equation and using the guess and check method we found that the maximum value for perimeter would be found when plugging in 0.5 as X and 15.75 as Y in P = 2 ( X + Y ). Our maximum value for perimeter is 32.5 and this can be verified by using our equation P = 2X^2 + 2X + 32. |
Group & Individual Tests
After completing this problem we were expected to take a group quiz and an individual quiz. In order to prepare for the group quiz my group and I decided to collectively work on a problem similar to the original. By doing this we were able to make sure we all understood the process of reaching a solution to this problem, were able to clearly write out the steps we took, and be able to complete the problem within a reasonable amount of time.
When my group was presented with the quiz I feel as though we worked very well together to understand and take on the problem. Every group member was able to contribute their ideas at some point during the quiz. Despite us not doing well on the accuracy of the problem we were able to comprehend the problem and came close to having our answers be correct.
My ability to understand the individual quiz was great and can be seen from my score of 30/30. While taking the quiz I felt confident in the work I was doing and in my awnsers. My overall experience while taking both quizzes was positive. My group and I worked well together and I felt prepared for the quizzes.
When my group was presented with the quiz I feel as though we worked very well together to understand and take on the problem. Every group member was able to contribute their ideas at some point during the quiz. Despite us not doing well on the accuracy of the problem we were able to comprehend the problem and came close to having our answers be correct.
My ability to understand the individual quiz was great and can be seen from my score of 30/30. While taking the quiz I felt confident in the work I was doing and in my awnsers. My overall experience while taking both quizzes was positive. My group and I worked well together and I felt prepared for the quizzes.
Reflection
If I were to grade myself on this unit I would receive an A. This is because of my leadership experience throughout the unit and my ability to push myself to understand the problem. Since the beginning of the unit I had taken on the role of a leader in my group. I was always on the board drawing out my groups ideas and solutions, asking questions, and clarifying steps to my group members to make sure we all understood the problem. By doing this I not only ensured that my group did well with the problem but I also bettered my ability to understand the problem. By articulating the steps we took and drawing out the steps it made taking on the quizzes less intimidating. Now I know that this method helps me study and potentially understand future problems.